Casca esférica carregada (TA-Fis3) #1

Campo elétrico produzido no interior de uma casca esférica (PARTE 1): como provar que a intensidade do campo elétrico na região é zero?

Este cálculo é facilmente demonstrado por meio da lei de Gauss, mas percebo que muitos alunos não se sentem confortáveis com a resposta dada por esse método. Talvez seja porque a técnica utiliza o conceito de fluxo elétrico, que não é algo muito intuitivo para a maioria dos estudantes, que veem muito mais clareza no resultado obtido por meio da lei de Coulomb. Assim, vamos discutir este assunto utilizando o processo de integração, por mais que isso possa gerar uma caminhada muito mais difícil do ponto de vista algébrico.

Considere uma casca esférica de raio r e espessura desprezível, com densidade superficial uniforme de carga \sigma e carga total q. Com este modelo, calcularemos o vetor campo elétrico em um ponto P localizado no eixo z, em uma distância z do ponto O (centro da esfera), conforme apresenta a figura abaixo. Além dos três eixos o sistema cartesiano, a figura também apresenta o eixo w que tem a mesma direção da projeção do vetor r sobre o plano xy.

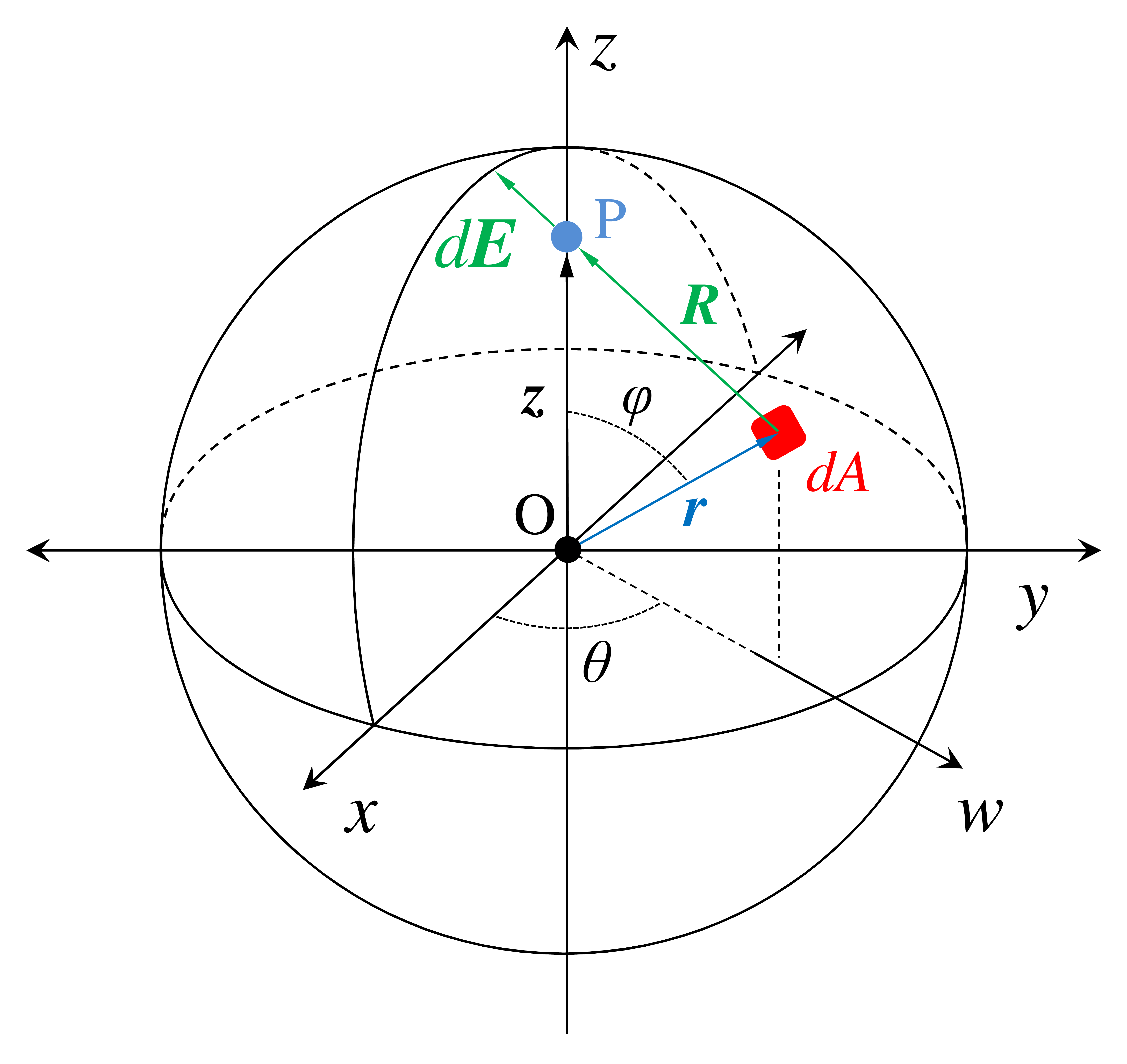
Figura 1. Casca esférica eletricamente carregada.

Para melhorar a visualização do problema, considere apenas o plano zw apresentado na figura abaixo. O elemento de campo elétrico d\vec{E} possui um elemento de carga simétrico, o que permite mostrar que o elemento de campo elétrico resultante d\vec{E}_R está na direção z.

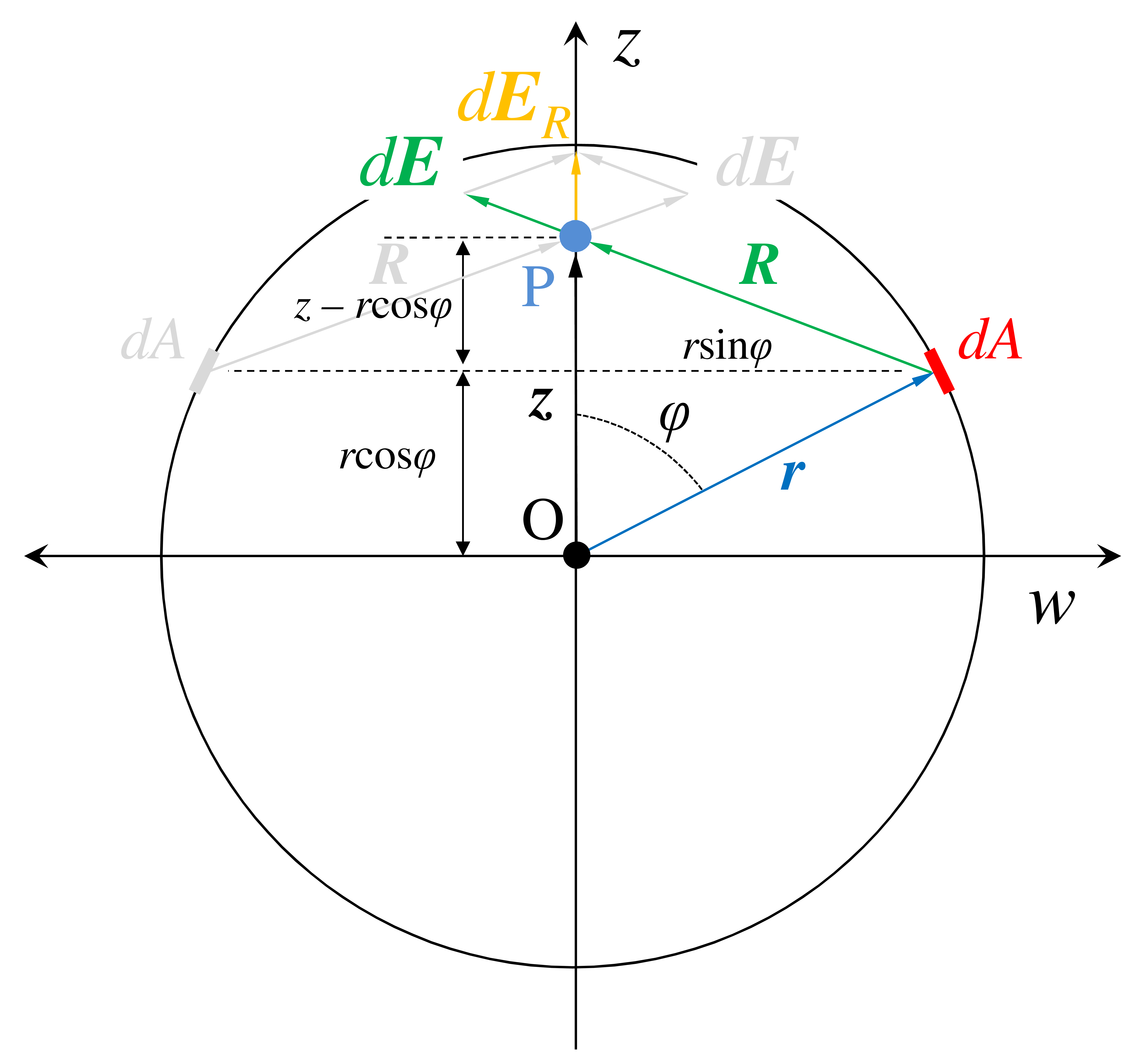
Figura 2. Plano zw da esfera apresentada na Figura 1.

O vetor distância \vec{R} do elemento de área dA até o ponto P é dado por:

\vec{R}=\vec{z}-\vec{r}= z\hat{k} - (r\cos{\varphi})\hat{k} - (r\sin{\varphi})\hat{w}
\\
(1) \vec{R}= - (r\sin{\varphi})\hat{w} + (z - r\cos{\varphi})\hat{k}

O módulo da equação 1 é dado por:

R^2= (- r\sin{\varphi})^2 + (z - r\cos{\varphi})^2
\\
R^2= r^2\sin^2{\varphi} + z^2 - 2zr\cos{\varphi} + r^2\cos^2{\varphi}
\\
R^2= r^2 + z^2 - 2zr\cos{\varphi}
\\
(2) R = \sqrt{r^2 + z^2 - 2zr\cos{\varphi}}

Logo, o elemento de campo elétrico d\vec{E} é dado por:

d\vec{E} = {\displaystyle \frac{dq}{4\pi\epsilon_0 R^2}\hat{R} = \frac{dq}{4\pi\epsilon_0 R^3}\vec{R} = \frac{\sigma dA}{4\pi\epsilon_0 R^3}\vec{R}}
\\
d\vec{E} = {\displaystyle \frac{\sigma r^2\sin{\varphi}d\varphi d\theta}{4\pi\epsilon_0\sqrt{r^2 + z^2 - 2zr\cos{\varphi}}}\left[-(r\sin{\varphi})\hat{w} + (z - r\cos{\varphi})\hat{k}\right]}

em que r é constante (condição de existência da casca esférica), 0 \leq \varphi \leq \pi e 0 \leq \theta \leq 2\pi:

(3)  \vec{E} = {\displaystyle \frac{\sigma }{4\pi\epsilon_0}\left(-\int_0^{2\pi}\int_0^{\pi}\frac{r^3\sin^2{\varphi}d\varphi d\theta}{\sqrt{r^2 + z^2 - 2zr\cos{\varphi}}}\hat{w} + \int_0^{2\pi}\int_0^{\pi}\frac{r^2\sin{\varphi}(z - r\cos{\varphi})d\varphi d\theta}{\sqrt{r^2 + z^2 - 2zr\cos{\varphi}}}\hat{k}\right)}

Podemos realizar a integração direta da equação 3 em d\theta:

(4)  \vec{E} = {\displaystyle \frac{\sigma}{2\epsilon_0}\left(- \underbrace{\int_0^{\pi}\frac{r^3\sin^2{\varphi}d\varphi}{\sqrt{r^2 + z^2 - 2zr\cos{\varphi}}}}_{I}\hat{w} + \underbrace{\int_0^{\pi}\frac{r^2\sin{\varphi}(z - r\cos{\varphi})d\varphi}{\sqrt{r^2 + z^2 - 2zr\cos{\varphi}}}}_{II}\hat{k}\right)}

Ambas as integrais da equação 4 são demasiadamente complexas; entretanto, a integral I é zero, pois ela representa a componente w do campo elétrico. Você consegue resolvê-la? A integral II pode ser resolvida com um pouco menos de álgebra por meio da substituição u = \cos{\varphi} (recomendo a tentativa). Porém, podemos resolver o mesmo problema com menos trabalho por meio do cálculo do potencial elétrico produzido por dA em P:

dV = {\displaystyle \frac{dq}{4\pi\epsilon_0 R} = \frac{\sigma r^2 \sin{\varphi} d\varphi d\theta}{4\pi\epsilon_0 \sqrt{r^2 + z^2 - 2zr\cos{\varphi}}}}
\\
V = {\displaystyle \frac{\sigma r^2}{4\pi\epsilon_0} \int_0^{2\pi}\int_0^{\pi}\frac{ \sin{\varphi} d\varphi d\theta}{\sqrt{r^2 + z^2 - 2zr\cos{\varphi}}}}
\\
(5) V = {\displaystyle \frac{\sigma r^2}{2\epsilon_0} \int_0^{\pi}\frac{\sin{\varphi} d\varphi}{\sqrt{r^2 + z^2 - 2zr\cos{\varphi}}}}

A equação 5 pode ser resolvida por meio da substituição:

(6) u = r^2 + z^2 - 2zr\cos{\varphi}

(7) du = 2zr\sin{\varphi}d\varphi

Substituindo as equações 6 e 7 em 5, obtemos:

V = {\displaystyle \frac{\sigma r^2}{2\epsilon_0} \int_0^{\pi}\frac{\sin{\varphi} d\varphi}{\sqrt{r^2 + z^2 - 2zr\cos{\varphi}}} = \frac{\sigma r}{4\epsilon_0 z} \int_{r^2 + z^2 - 2zr}^{r^2 + z^2 + 2zr}\frac{du}{u^{1/2}} = \frac{\sigma r}{2\epsilon_0 z}u^{1/2}\biggr\rvert_{r^2 + z^2 - 2zr}^{r^2 + z^2 + 2zr}}
\\
(8) V = {\displaystyle \frac{\sigma r}{2\epsilon_0 z}\left[\sqrt{r^2 + z^2 + 2zr} - \sqrt{r^2 + z^2 - 2zr}\right] = \frac{\sigma r}{2\epsilon_0 z}\left[\sqrt{(r+z)^2} - \sqrt{(r-z)^2}\right]}

A equação 8 pode ser escrita no formato modular:

(9) V = {\displaystyle \frac{\sigma r}{2\epsilon_0 z}\left(|r+z| - |r-z|\right)}

Os dois módulos da equação 9 significam que estes valores são sempre positivos e para que isso seja verdade fora da esfera, devemos ter z > r. Considerando que a densidade superficial de carga da esfera é \sigma = q/4\pi r^2, obtemos:

V = {\displaystyle \frac{\sigma r}{2\epsilon_0 z}\left[(r+z) - (z-r)\right]=\frac{\sigma r^2}{\epsilon_0 z}=\frac{q r^2}{4\pi r^2 \epsilon_0 z}}

(10)  \boxed{ V(z) = {\displaystyle \frac{q }{4\pi \epsilon_0 z}}} (z > r: potencial elétrico fora da esfera)

que é o mesmo potencial elétrico produzido por uma carga pontual. Assim, concluímos que o potencial elétrico produzido fora de um corpo com raio não desprezível é o mesmo do produzido por uma carga pontual. Para dentro da esfera (z < r), a equação 9 é dada por:

V = {\displaystyle \frac{\sigma r}{2\epsilon_0 z}\left[(r+z) - (r-z)\right] = \frac{\sigma r}{2\epsilon_0 z}}(2z)
\\
V = {\displaystyle \frac{\sigma r}{\epsilon_0} = \frac{q r}{4\pi r^2 \epsilon_0}}
\\
(11)  \boxed{ V = {\displaystyle \frac{q}{4\pi \epsilon_0 r}}} (z < r: potencial elétrico dentro da esfera)

As equações 10 e 11 explicam o comportamento do potencial elétrico para z > r ou z < r, respectivamente. Em z = r existe um problema de fronteira e apesar da equação 9 fornecer um resultado coerente, é necessário problematizar um modelo com casca de espessura não desprezível para melhor avaliação do resultado neste ponto (confira essa discussão na PARTE 2). O resultado da equação 11 mostra que o potencial elétrico dentro da casca esférica é constante, i.e., o espaço é equipotencial. Como não existe diferença de potencial entre dois pontos quaisquer, concluímos que o campo elétrico na região é zero, indicando que a soma de todos os elementos de campo no ponto P é nula. Podemos comprovar este resultado por meio do cálculo do campo elétrico a partir da aplicação do operador gradiente [1, 2]:

\vec{E} = - \vec{\nabla} V

Considerando a coordenada z na direção radial, obtemos:

(12) \boxed{\vec{E}(z) = {\displaystyle \frac{q }{4\pi \epsilon_0 z^2}\hat{k}}} (z > r: campo elétrico fora da esfera)

(13) \boxed{ E = 0} (z < r: campo elétrico dentro da esfera)

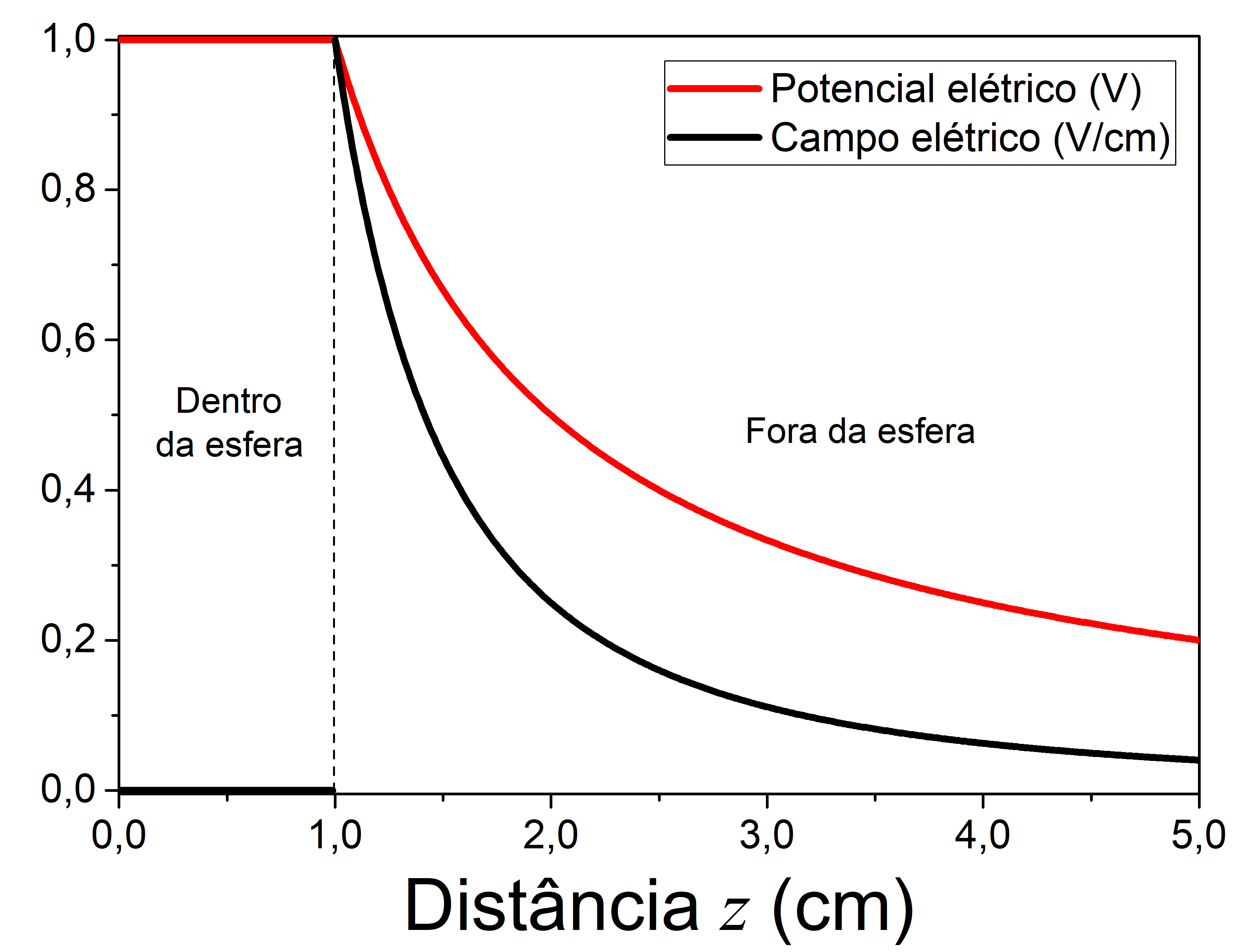
mostrando que o campo elétrico produzido dentro da casca é nulo, i.e., os vetores se anulam em qualquer ponto da região. O comportamento gráfico das equações 10, 11, 12 e 13 são apresentados na figura abaixo. Para isso, considerei uma esfera com raio de 1 cm e q/4\pi\epsilon_0 = 1 V\cdotcm.

Referências

[1] NUSSENZVEIG, H. M. Curso de Física Básica 3: Eletromagnetismo. 1. ed. São Paulo: Edgard Blucher, 1997.

[2] DUARTE, D. A., Videoaula: Campo elétrico obtido pelo potencial.
Disponível em https://www.youtube.com/watch?v=qAOnJgU9C70&t=4700s.

                                    

                                        
            


                    
    
        
    
        



	


	







    

        
        
        
    






    
    
        
  •  Desenvolvido com o CMS de código aberto Wordpress
    • 
        
  • Última atualização do site foi em 24 de agosto 2024 - 22:15:31
    •