Casca esférica carregada (TA-Fis3) #2

Campo elétrico produzido no interior de uma casca esférica (PARTE 2): qual é a influência da espessura da casca na intensidade do campo elétrico?

Na PARTE 1 discutimos o problema do campo elétrico produzido dentro e fora de uma casca esférica carregada com densidade superficial de carga \sigma. Neste exemplo, vamos discutir o mesmo problema; porém, considerando uma casca de espessura não desprezível. A ideia é compreendermos o comportamento do potencial e campo elétrico dentro da casca. O cálculo do campo elétrico é facilmente demonstrado com a Lei de Gauss, mas assim como fizemos anteriormente, faremos uma caminhada maior por meio de integração. O procedimento abaixo é interessante quando desejamos fortalecer a base matemática do cálculo, pois não é muito comum trabalharmos com integração de funções modulares na graduação, conforme veremos a seguir.

Para resolvermos o problema por integração, considere uma casca esférica de espessura t não desprezível:

(1) t = b - a

em que b é o raio externo da casca e a o raio interno, conforme ilustra a Figura 1.

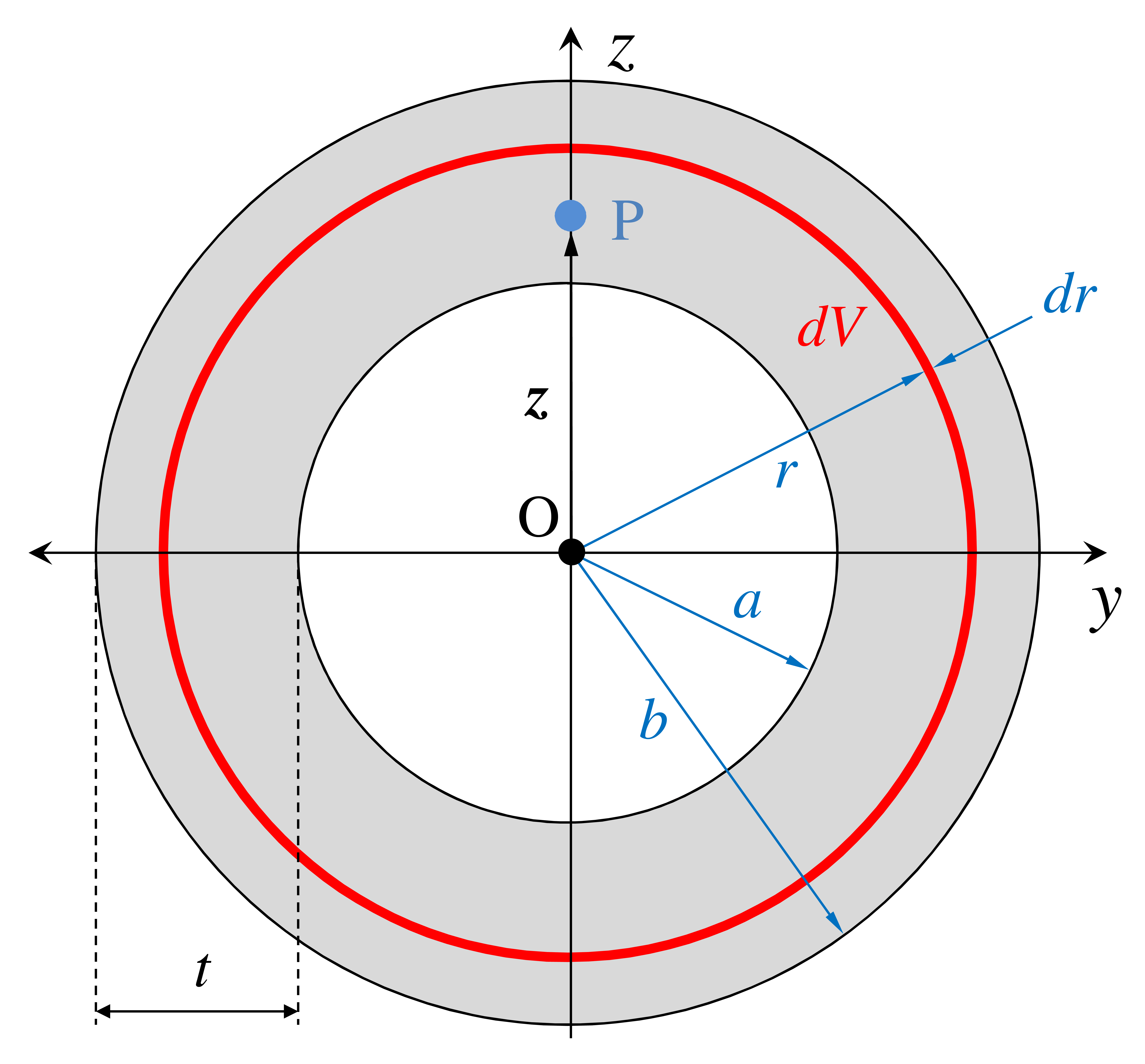
Figura 1. Representação esquemática de uma casca esférica de espessura não-desprezível

Com isso, devemos atribuir uma densidade volumétrica de carga \rho para o corpo:

(2) {\displaystyle \rho = \frac{q}{\frac{4}{3}\pi (b^3-a^3)} = \rho = \frac{3q}{4\pi (b^3-a^3)}}

em que q é a carga elétrica total. Para o cálculo do campo elétrico, vamos considerar que o corpo é formado por infinitas cascas esféricas concêntricas. Assim, podemos partir do resultado obtido na PARTE 1 para o potencial elétrico:

(3) V = {\displaystyle \frac{\sigma r}{2\epsilon_0 z}\left(|r+z| - |r-z|\right)}

em que \sigma deve ser reescrito em função de \rho. Para isso, considere o volume da casca esférica que pode ser reescrito em função da fatoração dos termos cúbicos:

(4) {\displaystyle V = \frac{4}{3} \pi (b^3-a^3) = \frac{4}{3} \pi (b-a)(b^2+ba+a^2)}

Substituindo b = t + a (equação 1) na equação 4, obtemos:

(5) {\displaystyle V = \frac{4}{3} \pi (b-a)(b^2+ba+a^2) = \frac{4}{3} \pi t(t^2 + 3at + 3a^2)}

O elemento de volume dV da casca (em vermelho na figura acima) é obtido a partir da derivada da equação 5 em relação à espessura t:

{\displaystyle \frac{dV}{dt} = \frac{4}{3}\pi(t^2+3at+3a^2) + \frac{4}{3}\pi t(2t+3a) = \frac{4}{3}\pi(3t^2+6at+3a^2)}
\\
{\displaystyle \frac{dV}{dt} = 4\pi(t^2+2at+a^2) = 4\pi(t+a)^2}
\\
{\displaystyle dV = 4\pi[(t+a)^2]dt}

Considerando que t \ll a para a casca de volume dV, obtemos {\displaystyle dV \approx 4\pi a^2dt}. Considerando dt = dr na figura acima, obtemos:

(6) {\displaystyle dV \approx 4\pi a^2 dr}

Com a equação 6 é possível escrever a densidade volumétrica de carga da seguinte forma:

{\displaystyle \rho = \frac{dq}{dV} = \frac{dq}{4\pi a^2 dr}}

em que dq é a carga elétrica da casca de espessura dr. O termo dq/4\pi a^2 representa a densidade superficial de carga; portanto:

{\displaystyle \rho = \frac{\sigma}{dr}}

o que permite escrever:

(7) \sigma = \rho dr

Substituindo a equação 7 na equação 3 podemos calcular o potencial elétrico que a casca de espessura dr produz em P:

dV = {\displaystyle \frac{\rho r}{2\epsilon_0 z}\left(|r+z| - |r-z|\right)dr}
\\
(8) V = {\displaystyle \frac{\rho}{2\epsilon_0 z}\int\left(r|r+z| - r|r-z|\right)dr}

A equação 8 deve ser resolvida sempre considerando que o resultado dos termos dentro do módulo seja sempre positivo. Isso implica em três condições para análise deste problema:

  1. A coordenada z está fora da esfera ou sobre sua superfície externa: esta condição significa que z \geq b e como o termo |r-z| da equação 8 deve ser positivo, aplicamos |r-z| = (z-r) com r integrado no intervalo a \leq r \leq b.
  2. A coordenada z está dentro da esfera ou sobre sua superfície interna (região de vácuo): esta condição significa que z \leq a e como o termo |r-z| da equação 8 deve ser positivo, aplicamos |r-z| = (r-z) com r integrado no intervalo a \leq r \leq b.
  3. A coordenada z está dentro da casca: esta condição significa que a \leq z \leq b e como o termo |r-z| da equação 8 deve ser positivo, aplicamos |r-z| = (r-z) com r integrado no intervalo z \leq r \leq b e |r-z| = (z-r) com r integrado no intervalo a \leq r \leq z. Este cálculo deve separar a equação 8 em duas integrais.

O potencial elétrico fora da esfera (z \geq b) é dado por:

(9) V = {\displaystyle \frac{\rho}{2\epsilon_0 z}\int_a^b\left[r(r+z) - r(z-r)\right]dr = \frac{\rho}{2\epsilon_0 z}\int_a^b\left[r^2+rz - rz+r^2\right]dr = \frac{\rho}{\epsilon_0 z}\int_a^b r^2 dr = \frac{\rho}{3\epsilon_0 z} (b^3-a^3)}

Substituindo a equação 2 em 9, obtemos:
\\
{\displaystyle V = \frac{q}{\frac{4}{3}\pi 3\epsilon_0 z (b^3-a^3)} (b^3-a^3)}

(10)  \boxed{{\displaystyle V(z) = \frac{q}{4\pi\epsilon_0 z}}} (potencial elétrico fora da casca)

que é o potencial elétrico produzido por uma partícula pontual, em acordo com o que calculamos na PARTE 1. Para dentro da esfera na região de vácuo (z \leq a), o potencial elétrico é dado por:

(11) V = {\displaystyle \frac{\rho}{2\epsilon_0 z}\int_a^b\left[r(r+z) - r(r-z)\right]dr = \frac{\rho}{2\epsilon_0 z}\int_a^b\left[r^2+rz + rz - r^2\right]dr = \frac{\rho}{\epsilon_0}\int_a^b r dr = \frac{\rho}{2\epsilon_0} (b^2-a^2)}

Substituindo a equação 2 em 11, obtemos:

{\displaystyle V = \frac{q}{\frac{4}{3}\pi 2\epsilon_0 (b^3-a^3)} (b^2-a^2)}
\\
(12)  \boxed{{\displaystyle V = \frac{3q}{8\pi\epsilon_0}\left(\frac{b^2-a^2}{b^3-a^3}\right) = \frac{3}{2}\left(\frac{q}{4\pi\epsilon_0}\right)\left(\frac{b^2-a^2}{b^3-a^3}\right)}}  (potencial elétrico dentro da casca na região de vácuo)

A equação 12 pode ser reescrita a partir da fatoração dos termos quadráticos e cúbicos que estão entre parênteses e a substituição b = t+a (equação 1):

{\displaystyle V = \frac{3q}{8\pi\epsilon_0}\left[\frac{(b-a)(b+a)}{(b-a)(b^2+ba+a^2)}\right] = \frac{3q}{8\pi\epsilon_0}\left[\frac{b+a}{b^2+ba+a^2}\right] = \frac{3q}{8\pi\epsilon_0}\left[\frac{(t+a)+a}{(t+a)^2+(t+a)a+a^2}\right]}
\\
{\displaystyle V(t) = \frac{3q}{8\pi\epsilon_0}\left(\frac{2a+t}{t^2+3at+3a^2}\right)}

que pode ser reescrita como:

(13)  \boxed{{\displaystyle V(t) = \frac{3}{2} \left(\frac{q}{4\pi\epsilon_0}\right)\left(\frac{2a+t}{t^2+3at+3a^2}\right)}}  (potencial elétrico dentro da casca na região de vácuo)

Podemos reescrever a equação 13 colocando a em evidência no numerador e denominador do segundo termo entre parênteses:

{\displaystyle V(t) = \frac{3}{2} \left(\frac{q}{4\pi\epsilon_0}\right)\frac{a}{a^2}\left[\frac{2+\left(\frac{t}{a}\right)}{\left(\frac{t^2}{a^2}\right)+\frac{3t}{a}+3}\right]}

e aplicando a condição para uma casca esférica de espessura desprezível (t \ll a):

  • {\displaystyle \frac{t}{a} \approx 0}
  • {\displaystyle \frac{t^2}{a^2} \approx 0}
  • {\displaystyle \frac{3t}{a}+3 \approx 3}

obtemos a seguinte expressão:

(14)  \boxed{{\displaystyle V = \frac{3}{2} \left(\frac{q}{4\pi\epsilon_0}\right)\left(\frac{2}{3a}\right) = \frac{q}{4\pi\epsilon_0 a}}}  (potencial elétrico dentro de uma casca esférica muito fina)

que é o potencial elétrico encontrado na PARTE 1 para a região interna de uma casca esférica com espessura desprezível. Com este resultado, podemos assegurar que as equações 12 e 13 estão corretas ao descrever o potencial elétrico na região interna de uma casca esférica com espessura qualquer. Podemos também utilizar a equação 13 para avaliar a condição t \gg a. Este caso indica que b \gg a, o que significa que estamos aproximando a casca esférica de uma esfera maciça, em que t é aproximadamente o raio da esfera. Para obter uma expressão do potencial elétrico nesta condição, vamos reescrever a equação 13 colocando t em evidência no numerador e denominador do segundo termo entre parênteses:

{\displaystyle V(t) = \frac{3}{2} \left(\frac{q}{4\pi\epsilon_0}\right)\frac{t}{t^2}\left[\frac{\left(\frac{2a}{t}\right)+1}{1+\frac{3a}{t}+\left(\frac{3a^2}{t^2}\right)}\right]}

e aplicar a condição t \gg a:

  • {\displaystyle \frac{2a}{t} \approx 0}
  • {\displaystyle \frac{3a^2}{t^2} \approx 0}
  • {\displaystyle 1+\frac{3a}{t} \approx 1}

o que resulta na equação:

(15)   \boxed{{\displaystyle V(t) \approx \frac{3}{2} \left(\frac{q}{4\pi\epsilon_0}\right)\left(\frac{1}{t}\right) \approx \frac{3}{2} \left(\frac{q}{4\pi\epsilon_0 t}\right)}}  (potencial elétrico no centro de uma esfera maciça)

Este mesmo resultado pode ser obtido com a resolução do problema 6 que está na minha lista de exercícios sobre potencial elétrico [1, 2]. Para chegar neste resultado basta calcular o potencial elétrico até o centro da esfera. O fator 3/2 representa a contribuição do potencial elétrico calculado do infinito até a superfície da esfera (67% de contribuição) e a contribuição do potencial elétrico calculado da superfície da esfera até seu centro (33% de contribuição) [2]. Como as equações 12, 13, 14 e 15 não dependem da distância z, o potencial é sempre constante na região interna, mostrando que o campo elétrico é sempre zero, independentemente da espessura da casca. A Figura 2 apresenta o comportamento gráfico da equação 13 em função da razão t/a. Para fins de simplificação do modelo foi adotado q/4\pi\epsilon_0 = 1 V\cdotcm e a=1 cm. Os dados mostram que as equações 14 e 15 são satisfeitas para t/a \ll 1 e t/a \gg 1, respectivamente, com uma visualização clara dos três modelos possíveis para estudo (casca com espessura desprezível, casca com espessura não-desprezível e esfera maciça).

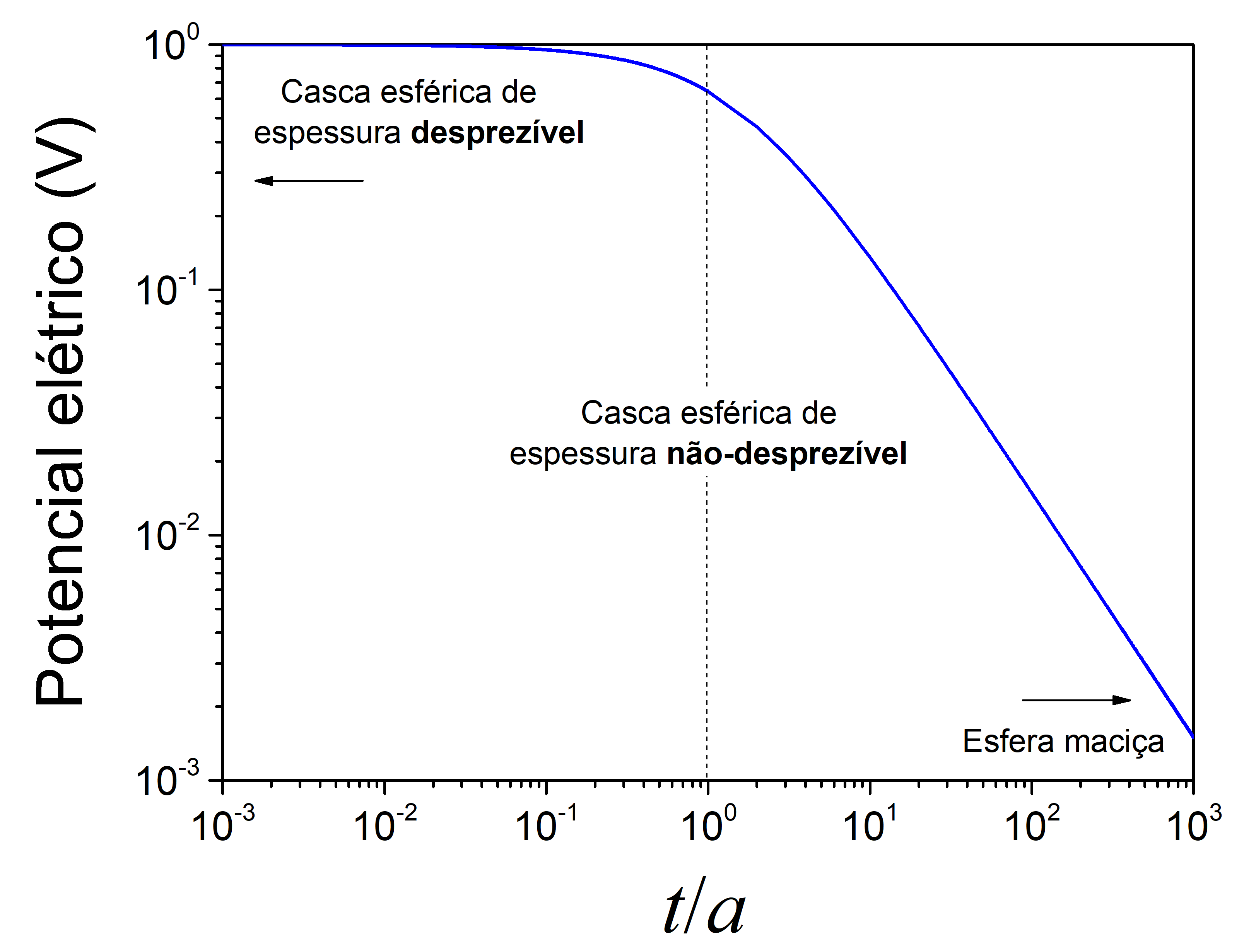
Figura 2. Potencial elétrico dentro da casca (região de vácuo) em função da razão t/a.

O potencial elétrico dentro da casca é dado por:

{\displaystyle V = \frac{\rho}{2\epsilon_0 z}\int_a^z \left[r|r+z|-r|z-r|\right]dr + \frac{\rho}{2\epsilon_0 z}\int_z^b \left[r|r+z|-r|r-z|\right]dr}

{\displaystyle V = \frac{\rho}{2\epsilon_0 z}\int_a^z \left[r(r+z)-r(z-r)\right]dr + \frac{\rho}{2\epsilon_0 z}\int_z^b \left[r(r+z)-r(r-z)\right]dr}

{\displaystyle V = \frac{\rho}{2\epsilon_0 z}\int_a^z \left(r^2+rz-rz+r^2\right)dr + \frac{\rho}{2\epsilon_0 z}\int_z^b \left(r^2+rz-r^2-rz\right)dr}

{\displaystyle V = \frac{\rho}{\epsilon_0 z}\int_a^z r^2 dr + \frac{\rho}{\epsilon_0}\int_z^b r dr}

(16)  \boxed{{\displaystyle V(z) = \frac{\rho}{3\epsilon_0 z}(z^3-a^3) + \frac{\rho}{2\epsilon_0}(b^2-z^2)}}   (potencial elétrico dentro da casca esférica)

Para validar a equação 16 vamos aplicá-la nas condições de fronteira:

{\displaystyle V(a) = \frac{\rho}{3\epsilon_0 z}(a^3-a^3) + \frac{\rho}{2\epsilon_0}(b^2-a^2) = \frac{\rho}{2\epsilon_0}(b^2-a^2)}

que é o mesmo resultado obtido para z \leq a na equação 11. Similarmente para z = b temos:

{\displaystyle V(b) = \frac{\rho}{3\epsilon_0 z}(b^3-a^3) + \frac{\rho}{2\epsilon_0}(b^2-b^2) = \frac{\rho}{3\epsilon_0 z}(b^3-a^3)}

que é o mesmo resultado obtido para z \geq b na equação 9. Portanto, podemos assegurar que a equação 16 descreve o potencial elétrico corretamente dentro da casca. Substituindo a equação 2 na 16, obtemos uma expressão em função da carga total:

{\displaystyle V(z) = \frac{q}{4\pi\epsilon_0 z}\left(\frac{z^3-a^3}{b^3-a^3}\right) + \frac{3}{2}\frac{q}{4\pi\epsilon_0}\left(\frac{b^2-z^2}{b^3-a^3}\right)}

(17)  \boxed{{\displaystyle V(z) = \frac{q}{4\pi\epsilon_0}\left[\frac{1}{z}\left(\frac{z^3-a^3}{b^3-a^3}\right) + \frac{3}{2}\left(\frac{b^2-z^2}{b^3-a^3}\right)\right]}}  (potencial elétrico dentro da casca esférica)

Com as equações 10, 12 e 17 é possível traçar o gráfico do potencial elétrico ao longo da distância z, conforme ilustra a Figura 3. Neste caso, foi adotado q/4\pi\epsilon_0 = 1 V\cdotcm, a=1 cm e b=3 cm, com a coordenada z variando entre 0 e 5 cm.

Figura 3. Potencial elétrico em função da distância radial produzido por uma casca esférica de espessura não-desprezível.

O campo elétrico na região é dado diretamente pela aplicação do operador gradiente nas equações obtidas para o potencial elétrico:

(18) \vec{E}=-\vec{\nabla}V = \displaystyle{\begin{cases}0, & \textrm{para } z \leq a\\ \frac{q}{4\pi\epsilon_0 z^2}\left( \frac{z^3-a^3}{b^3-a^3} \right)\hat{z}, & \textrm{para }a \leq z \leq b\\ \frac{q}{4\pi\epsilon_0 z^2}\hat{z}, & \textrm{para } z \geq b \end{cases}}

Finalmente, a representação gráfica do campo elétrico é apresentada na Figura 4. O campo elétrico é zero dentro da casca, proporcional à distância radial dentro da região material da casca e inversamente proporcional à distância radial fora da casca. Para simplificação do modelo, foi considerada a permissividade elétrica do vácuo no meio material.

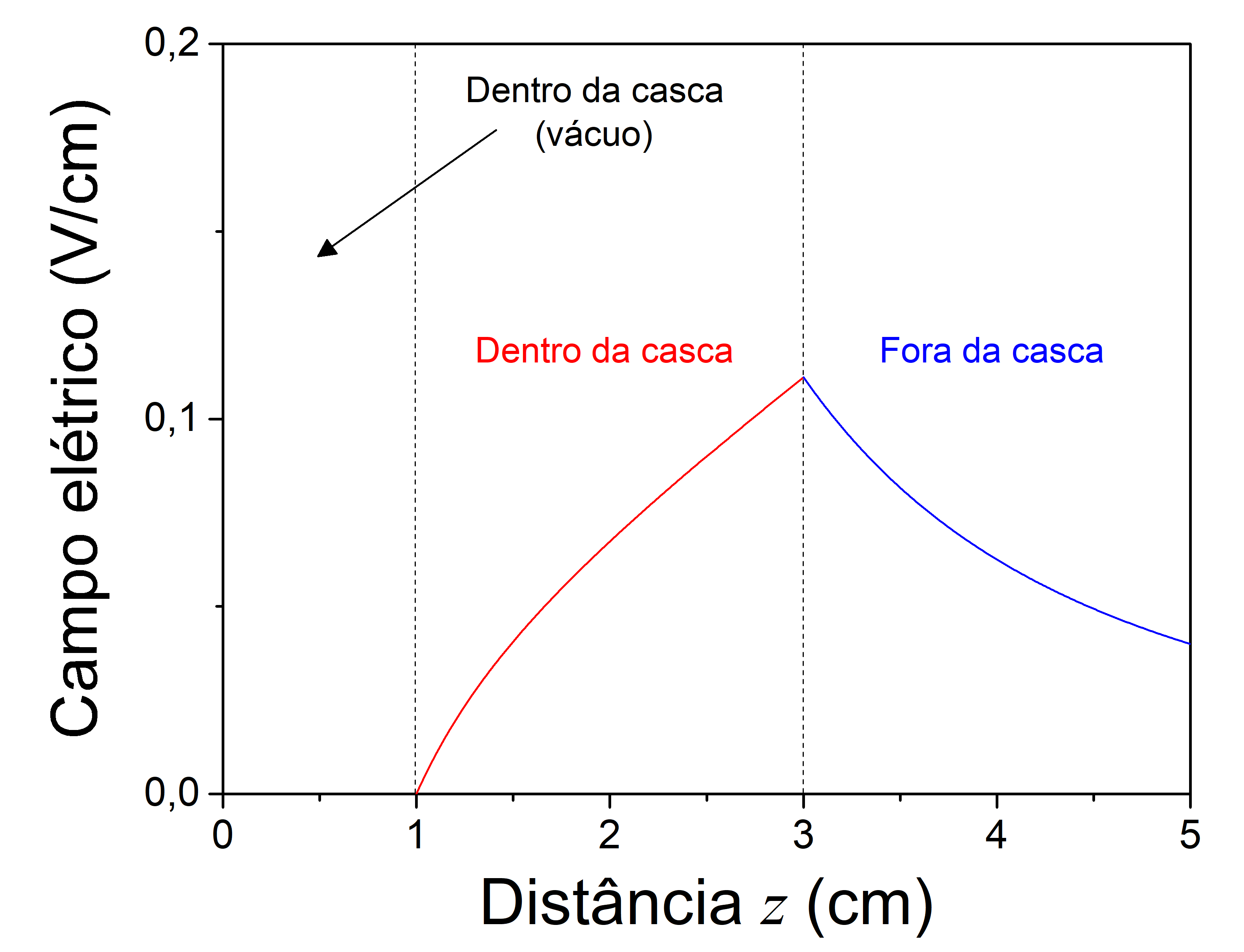
Figura 4. Campo elétrico em função da distância radial produzido por uma casca esférica de espessura não-desprezível.

A equação 18 pode ser ajustada para descrever o campo elétrico produzido por uma esfera. Para isso, basta aplicar a = 0 e substituir a equação 2:

(19) \vec{E}=-\vec{\nabla}V = \displaystyle{\begin{cases} \frac{\rho z}{3\epsilon_0}\hat{z}, & \textrm{para } z \leq b\\ \frac{\rho b^3}{3 \epsilon_0 z^2}\hat{z}, & \textrm{para } z \geq b \end{cases}}

Como disse no início desta discussão, os resultados das equações 18 e 19 também podem ser obtidos diretamente com a lei de Gauss [3, 4]. O campo elétrico em função da distância radial para diferentes valores da espessura da casca é apresentado na Figura 5 (descrição no meio material). Os dados mostram que não existe uma mudança descontínua do campo elétrico entre as regiões interna e externa da casca, conforme apresentado na PARTE 1. Existe uma função bem definida que descreve a transição entre as regiões, e que se torna mais abrupta conforme a espessura da camada é reduzida devido ao aumento da densidade volumétrica de carga na região (usei a equação 18 para traçar as curvas - que fixa o valor total da carga da esfera). O campo elétrico para t\gg a adquire valores pequenos; porém, aumenta linearmente com a coordenada z, conforme descrito pelo resultado da equação 19.

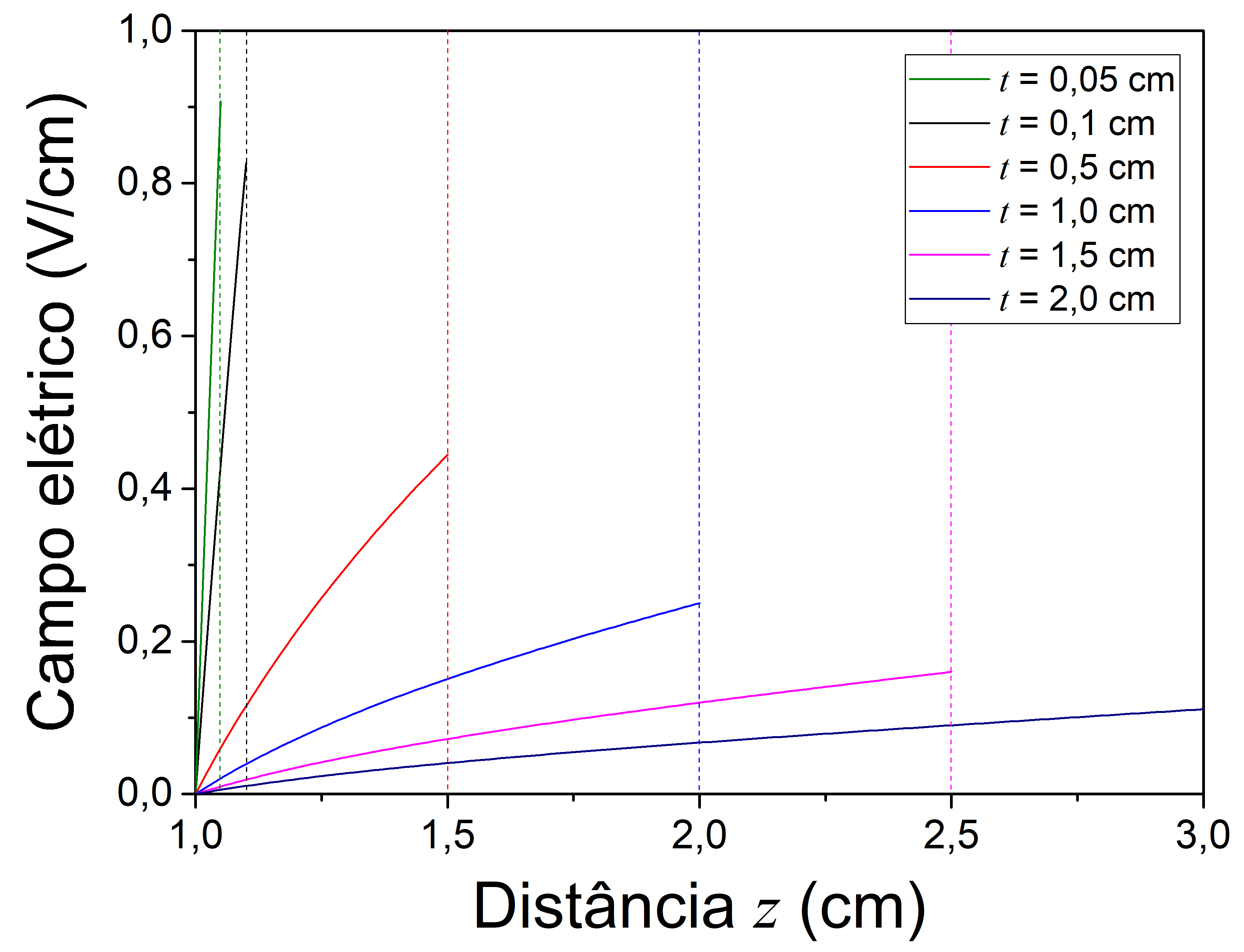
Figura 5. Campo elétrico em função da distância radial produzido no meio material da casca para diferentes valores de sua espessura.

Referências

[1] DUARTE, D. A., Lista 4 (Potencial Elétrico). Problema 6.
Disponível em https://diegoduarte.paginas.ufsc.br/lista-de-exercicios-fisica-3/.

[2] DUARTE, D. A., Videoaula: Potencial elétrico.
Disponível em https://www.youtube.com/watch?v=qAOnJgU9C70&t=6163s.

[3] NUSSENZVEIG, H. M. Curso de Física Básica 3: Eletromagnetismo. 1. ed. São Paulo: Edgard Blucher, 1997.

[4] DUARTE, D. A., Videoaula: Lei de Gauss.
Disponível em https://www.youtube.com/watch?v=BWtVdBIG0M4&t=3161s.

  • Desenvolvido com o CMS de código aberto Wordpress
  • Última atualização do site foi em 24 de agosto 2024 - 22:15:31